[コンプリート！] If X 2xy-y^2=2 Then At The Point (1 1) 163463

If x^2 2xy 2y^2 = 1, then dydx at the point where y = 1 is equal to Click here👆to get an answer to your question ️ If x^2 2xy 2y^2 = 1, then dydx at the point where y = 1 is equal to Join / Login >12th >Maths >Continuity and Differentiability >Derivatives of Implicit FunctionsX^2 2 y^2 = 1 Natural Language;Get an answer for '`x^2 2xy y^2 x = 2, (1, 2)` Use implicit differentiation to find an equation of the tangent line to the curve at the given point' and find homework help for other Math

Solved 2 7 8 Pts Find The Value Of Ox Az At The Point Chegg Com

If x 2xy-y^2=2 then at the point (1 1)

If x 2xy-y^2=2 then at the point (1 1)-If a curve y = f(x), passing through the point (1,2), 2x 2 2dy= (2xy y 2)dx, then f \(\Big(\frac{1}{2}\Big)\) is equal to jee main ;Algebra Solve by Substitution xy=1 , 2xy=2 x y = 1 x y = 1 , 2x − y = −2 2 x y = 2 Subtract y y from both sides of the equation x = 1− y x = 1 y 2x−y = −2 2 x y = 2 Replace all occurrences of x x with 1−y 1 y in each equation Tap for more steps Replace all occurrences of x x in 2 x − y = − 2 2 x y

2

Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepVisit to my Channel https//youtubecom/c/GRAVITYcoachingInstituteVisit to my Channel Playlist https//wwwyoutubecom/c/GRAVITYCOACHINGINSTITUTE/playlists I'd recommend that you think (and write) x^2 y^2 = 29, so the question get's rephrased as "What's the value of 29 2xy ?" At this point, it should be clear that statement 1 is sufficient, as it gives you the missing unknowns in the question as values if x = 5 then 29 2 (5)y = 29 10y 10y = 29 This is your real mistake

 1 Alpha identifies it as Legendre's equation and gives the solution y ( x) = c 1 x c 2 ( − x ( log ( 1 − x) / 2 − log ( x 1)) − 1) It offers step by step if you have the right account Share answered at 1348 Jul 17,22 The function f(x,y) = 2x2 2xy y3 hasa)Only one stationary point at (0,0) b)Two stationary points at (0,0) and (1/6, 1/3) c)Two stationary points at (0,0) and (1,1) d)No stationary pointCorrect answer is option 'B' Can you explain this answer?Y2 $ ∂g ∂v ·(2y) and at the point (x,y)=(1,1) we have u =(1/1,12 12)=(1,2) so that ∂G ∂x (1,1) = 3 ·14·2=11 ∂G ∂y (1,1) = 3 ·(−1) 4 ·2=5 (b) (5 pts) The equation xyzz3 =6implicitlydefinesz = z(x,y)asafunctionofx and yFind the value of ∂z ∂x at the point (−1,1,2)

The combined equation of two sides of a triangle is x 2 − 3 y 2 − 2 x y 8 y − 4 = 0 The third side, which is variable always passes through the point (− 5, − 1) If the range of values of the slope of the third line such that the origin is an interior point of the triangle is (a, b), then the value of (a 1X^2y^2=25 2x 2y\frac{dy}{dx}=0 \displaystyle\frac{dy}{dx} = \frac{x}{yBased on the general formula and concept Q Q1 Solve the following differential equation2x²y;

2

A Curve Has Equation Y E 1 2x 1 The Curve Crosses The Y Axis At Point P The Normal To The Curve At Point P Meets The X

Similar Questions Find the equation of circle having the lines \(x^2\) 2xy 3x 6y = 0 as its normal and having size just sufficient to contain the circle x(x – 4) y(y – 3) = 0 1 If 3x^22xyy2=2 then the value of dy/dx x = 1 is A 2 B 0 C 2 D 4 E not defined Calculus The line that is normal to the curve x^2=2xy3y^2=0 at(1,1) intersects the curve at what other point?Simplify x=y1 x=y1 Add y to both sides of the equation y^ {2}\left (2x\right)yx^ {2}1=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions,

2

Solved Question 1 If 3x2 2xy Y2 2 Then The Value Of Chegg Com

 If 3x^22xyy2=2 then the value of dy/dx x = 1 is A 2 B 0 C 2 D 4 E not defined Calculus Find an equation of the line tangent to the curve defined byA line parallel to the straight line 2xy = 0 is tangent to the hyperbola (x^2/4)(y^2/2) = 1 at the point (x_1, y_1) Then x_1^25y_1^2 is equal to Get the answer to this question and access more number of related questions that are tailored for studentsExplanation Given Expression 3x 2 2xy y 2 = 2 When x = 1 then y = 1 by substituting the value of x in the above expression Differentiating on both the sides of the given expression with respect to x, we get (d / dx) (3x 2 2xy y 2) = (d / dx) (2) ⇒ 6x 2 x dy / dx y 2y dy / dx = 0 d / dx (xy) = x dy/dx y using product rule of differentiation

Find Dydx Where X 2 Y 2 3xy 1

If A Curve Y F X Passing Through The Point 1 2 Is The Solution Of The Differential Sarthaks Econnect Largest Online Education Community

 If the pair of lines `x^(2)2xyay^(2)=0` and `ax^(2)2xyy^(2)=0` have exactly one line in common, then a = A `1` B `3` C `1` D 3 The equation of the straigh lines through the point `(x_(1),y_(1))` and parallel to the lines given by `ax^(2)2xyay^(2)=0`, is Statement1 If a, b are nonzero real number such that `ab=2`, then Explanation We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;1 See answer This is why I want to be a moderator, so this doesn't have to happen

2

2

Y = −02 12(1) = 1 As depicted in Fig 1411, we move to the new coordinates, labeled point 2 in the plot, and in so doing move closer to the maximum The approach can be repeated with the final result converging on the analytical solution, x = 2 and y = 1Click HERE to return to the list of problems SOLUTION 14 Begin with x2/3 y2/3 = 8 Differentiate both sides of the equation, getting (Remember to use the chain rule on D ( y2/3 ) ) so that (Now solve for y ' ) Since lines tangent to the graph will have slope $ 1 $ , set y ' =Consider the function f R 2 → R 2 given by f(x, y) = x 2 − 2xy y 4 − 4x 4y (a) Compute the gradient ∇f at a general point (x, y) and then at the point (2, 1) (b) Sketch the level curves f(x, y) = k for the values k = 1 and k = 4 (c) Compute the directional derivative of f at (2, 1) in the direction of the vector u = (3, 2)

2

If 3x 2 2xy 6y 2 6 Then Dy Dx At 1 1 Is

If x^2 2xy 2y^2 = 1, then dydx at the point where y = 1 is equal to Class 12 >> Maths >> Continuity and Differentiability >> Derivatives of Implicit Functions >> If x^2Answer (1 of 2) If x^2y^2=25, what is the value of \frac{d^2y}{dx^2} at the point (4,3)?Solution for 2xy y' x² y2 y (1) = 1 2 different methods Q (a) Apply first principles, to calculate the differential coefficient of r(x)= 5(3x² 2) when x = A Since you have asked multiple question, we will solve the first question for youIf you want any

Solutions To Homework Assignment 5 Math 253

What Is A Residue In Complex Analysis How Do We Find It Through The Laurent Series Of A Function And What S The Intuition Behind Finding It This Way Quora

Please help Thanks in advance We have x2=2xy 3y2 = 0 Are there supposed to be 2 equal signs in this expression or is it x2I = e∫P (x)dxKEAM 12 If x2 2xy 2y2 = 1, then (dy/dx) at the point where y = 1 is equal to (A) 1 (B) 2 1 (D) 2 (E) 0 Check Answer and Solution for above

1

If X Y 6 X Y 2 What Is The Value Of X And Y Quora

 2xy then the point 1,1 thanh simpleIf 2xy then the point 1,1 thanks jake Answerx 2xySOLUTION 1 Begin with x3 y3 = 4 Differentiate both sides of the equation, getting (Remember to use the chain rule on D ( y3 ) ) so that (Now solve for y ' ) Click HERE to return to the list of problems SOLUTION 2 Begin with ( x y) 2 = x y 1 Differentiate bothA tangent at a degree on the curve could be a straight line that touches the curve at that time and whose slope is up to the derivative of the curve at that point From the definition, you'll be able to deduce the way to realize the equation of the tangent to the curve at any point Given a function y = f(x), the equation of the tangent for this curve at x = x0

Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When

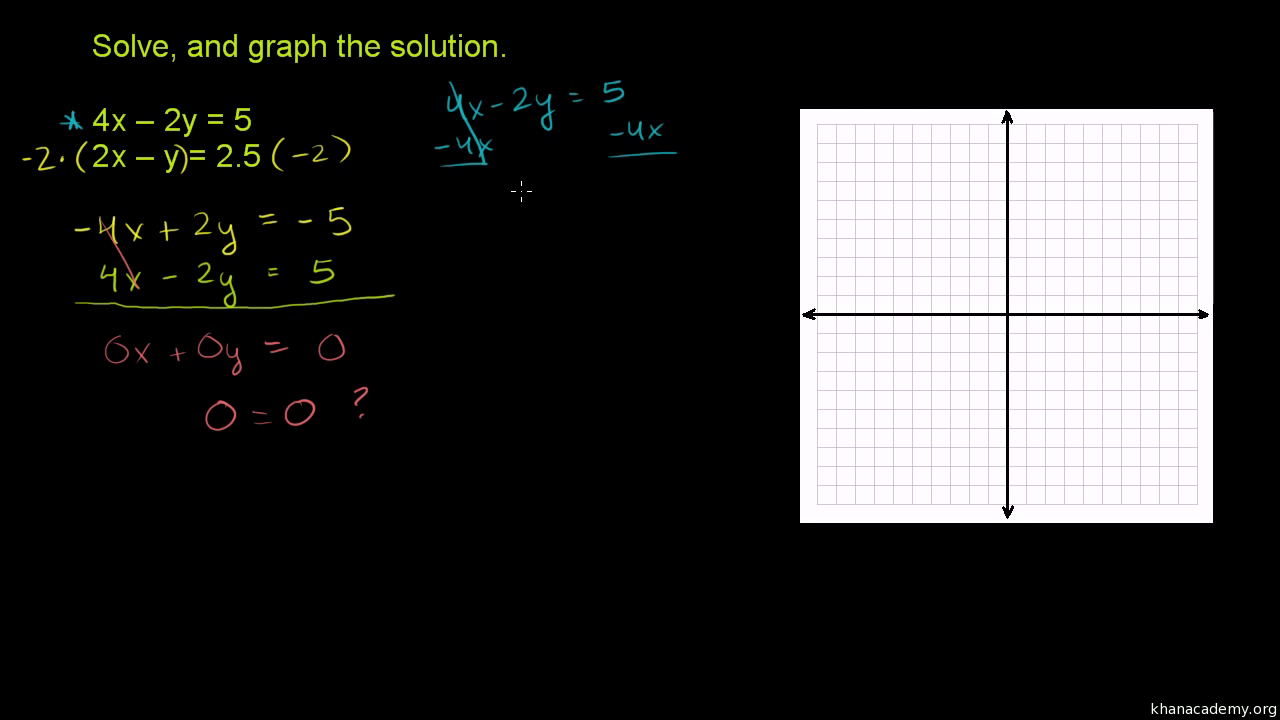
Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy

Answer Refer image Explanation The electric potential in space is given by V(x,y,z) = (2xy y²z x²yz) volt, where x,y and z are in metre Then y component of electric field at the point (3,2,1) will be The electric potential in space is given by V ( x , y , z ) = ( 2xy y²z x²yz ) volt , where x , y and z are in metreA will now lie on the locus of P, ie AS = AZ The xaxis will be along the line AS, and the yaxis will be along the perpendicular to AS at A, as in the figure By definition PM = PS => MP 2 = PS 2 So, (a x) 2 = (x a) 2 y 2 Hence, we can get the equation of horizontal parabola as y2 = 4axDy dx P (x)y = Q(x) We have y' − 2xy = 1 with y(0) = y0 1 This is a First Order Ordinary Differential Equation in Standard Form So we compute and integrating factor, I, using;

Guide 3

Functions Of Severable Variables

Point of Diminishing Return Fraction to Decimal Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time tangent of x^22xyy^2x=2, (1,2) Pre Algebra;Share It On be the solution of the differential equation cosx dy/dx 2y sin x = sin 2x, x ∈ (0, π/2) If y(π/3) = 0, then y( π/4) is equal to asked in Mathematics by Chandan01Divide y, the coefficient of the x term, by 2 to get \frac{y}{2} Then add the square of \frac{y}{2} to both sides of the equation This step makes the left hand side of the equation a perfect square

What Is The Angle Between The Lines Joining The Origin To The Point Of Intersection Of The Curve X 2 2xy Y 2 2x 2y 5 0 And The Line 3x Y 1 0 Quora

2

Then, $3499 USD per year until cancelledExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicAnd then we'll have plus free Y squared Why prime equal to zero And then we can keep doing this And when we evaluated at X equals one, we ended up seeing that 42 is the final answer

Jacobian Properties Find ꝺ U V ꝺ R 8 When U X 2 Y 2 V 2xy X Rcos8 Y Rsin8 Youtube

If X 2 Y 2 Xy 8 What Is The Value Of X 2 Y 2 Quora

Answer (1 of 3) I appears your vertex is at (1, 1) and your focus at (2, 2) which makes the directrix y = x Let (a, b) be a point on the parabola The distance to (2, 2) is sqrt((a 2)^2 (b 2)^2) The point on y = x closest to (a, b) is ((a b)/2, (b a)/2) so the distance from (a, b)Question If x^2yyx^2=6, then d^2y/dx^2 at the point (1,3) is (A) 18 (B) 6 6 (D) 12 (E) 18 Answer by Fombitz(323) (Show Source) YouNicky129 nicky129 Mathematics High School answered If x^2y3x=y^33, then at the point (1,2), (dy/dx)?

U Osu Edu

Find The Equation Of The Straight Line Which Cuts Off Intercepts On X Axis Twice That On Y Sxis And Is At A Unit Distance From The Origin

 Click here 👆 to get an answer to your question ️ If x^2y3x=y^33, then at the point (1,2), (dy/dx)?Y(1) = 2πycos y A Explanation of the answer is as follows Q Calculus I A Given,h(x)=x2f(g(x)) Q Given the equation z = arctan(x y²) with the change of variables x=s³t³EduRev Mechanical Engineering Question is disucussed on EduRev Study Group by 6524 Mechanical Engineering

2

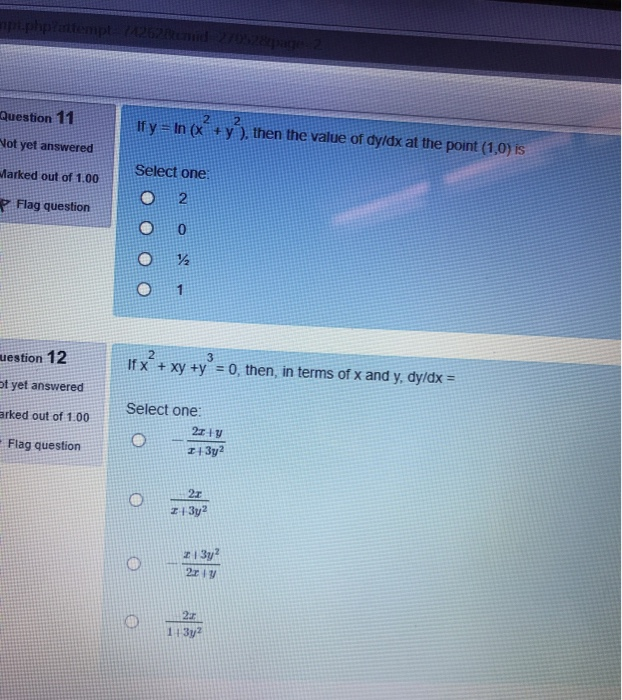
Solved Question 1 Not Yet Answered E 1 Lim 0 2h Is Marked Chegg Com

1 f(x;y) = (2xy x 2y (x;y) 6= (0 ;0) 0 (x;y) = (0;0) This function is NOT continuous at the origin If we approach it along the line y= 0 or x= 0 then If fhas a unique global maximum at a point a then the maximum value of fon a domain Doccurs at the point in Dclosest to a FALSE say f(x;y) = 10x2 y2 where Dis the line y= 1 x 5 ThereCalculus Find dy/dx x2xyy^2=2 x 2xy − y2 = 2 x 2 x y y 2 = 2 Differentiate both sides of the equation d dx (x2xy−y2) = d dx (2) d d x ( x 2 x y y 2) = d d x ( 2) Differentiate the left side of the equation Tap for more steps DifferentiateA) –1 B) 0 C) 1 D) –y E) y Found 2 solutions by palanisamy, Alan3354 Answer by palanisamy(496) (Show Source) You can put this solution on YOUR website!

How To Use Implicit Differentiation To Find Dy Dx Unfortunately 2xy Y 2 1 Quora

Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf

 If y is a differentiable function of x, then the slope of the curve of xy^2 2y 4y^3 = 6 at the point where y=1 is (Show work!) a 1/18 b 1/26 c 5/18 dQuestion 2526 If x^2 y^2 = 2xy, then x must equal ?Given, x^2 y^2 = 2xy x^2 y^2 2xy = 0 (xy)^2 = 0 (xy) = 0

M23a Fin S18v1 Final Math 23a Spring 18 Final Exam Ucsc Auerle Tromba Notes No Calculators Studocu

Sites Oxy Edu

 At (1,2), we get 2(1) 2(2) 2(1) dy dx − 2(2) dy dx 1 = 0 so 2 4 2 dy dx −4 dy dx 1 = 0 7 − 2 dy dx = 0 and finally dy dx = 7 2 The tangent line contains the point (1,2) and has slope m = 7 2 so its equation is y = 7 2x − 3 2 With experience, your solution will look more like x2 2xy −y2 x = 2

Which Is The Value Of 1 X 1 Y If X And Y Are Positive With X Y 2 And Xy 24 1 5 12 2 1 12 3 1 6 4 25 6 Quora

Solved Find The Equation Of The Tangent Plane The Suriace Z0 F 2 7 Atthe Point 1 1 3 For Purticular Function 2 3 16 2 3 5 And 6 2 3 7 Which Of The Following Approximations Valid Near 2 3 F I U

If X 2xy Y2 2 Then At The Point 1 1 Dy Dx Under Gauthmath

Lf The Axes Are Translated To The Point 2 3 Then The Equation X 2 3y 2 4x 18y 30 0 Transforms To

If X 2xy Y2 2 Then At The Point 1 1 Dy Dx Under Gauthmath

What Is The Equation Of The Tangent To The Parabola Y 2 4x At The Point 1 2 Quora

How To Use Implicit Differentiation To Find Dy Dx Unfortunately 2xy Y 2 1 Quora

14 2 Limits And Continuity

Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy

Solved Exercises 3 4 1 Use Implicit Differentiation To Find Chegg Com

If X 2 2xy 2y 2 1 Then Dydx At The Point Where Y 1 Is Equal To

2

2

If X 2 Sin 2 8 And Y 2 Cos 2 8 1 Then Find X Y Teachoo

Solved 2 7 8 Pts Find The Value Of Ox Az At The Point Chegg Com

Inflection Points Algebraic Video Khan Academy

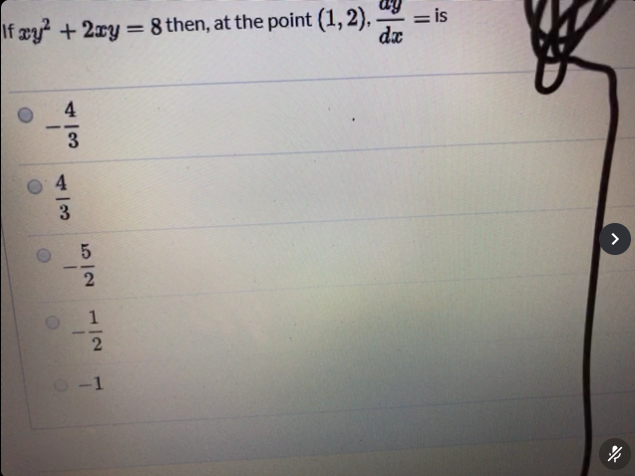
Solved If Xy 2 2xy 8x Y 2 2 X Y 8 Then At The Chegg Com

How We Do If X Y 2 Z 2 Y Z 2 X 2 And Z X 2 Y 2 Then Prove That X X 1 Y Y 1 Z Z 1 1 Quora

If X Y 2 And X Y 2 What Is The Value Of Xy Quora

If X 1 2x 2 What Is The Value Of 8x 3 1 X 3 Quora

How To Use Implicit Differentiation To Find Dy Dx Unfortunately 2xy Y 2 1 Quora

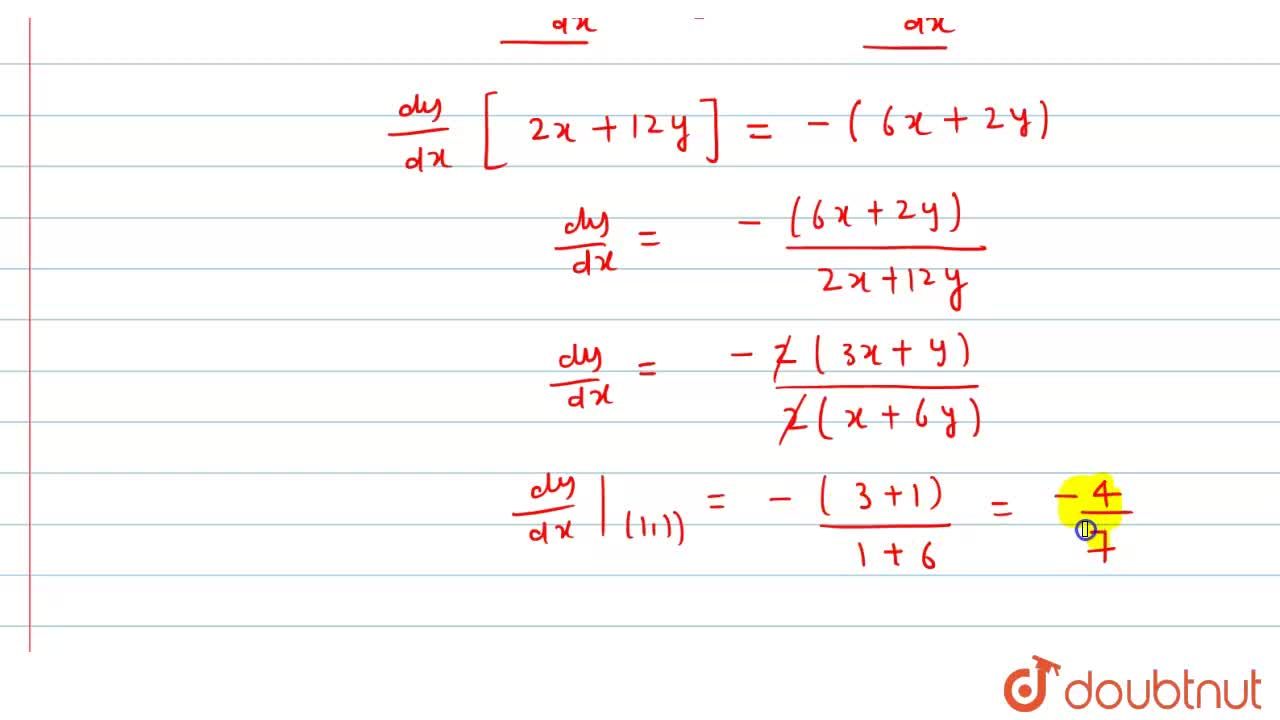
If 3x 2 2xy 6y 2 6 Then Dy Dx At 1 1 Is

What Is The Distance Of The Point 1 5 From The Line X Y Measured Parallel To The Line 3x Y 2 Quora

3 8 Implicit Differentiation Calculus Volume 1

2

Worked Example Implicit Differentiation Video Khan Academy

2

If X Y 3 X Y 1 Then What Is X Y Quora

Solved 1 Point Each Consider The Statement If X 2 Then X 2 4 A Course Hero

2

Solved Question 1 Not Yet Answered E 1 Lim 0 2h Is Marked Chegg Com

Systems Of Linear Equations

When The Origin Is Shifted To A Suitable Point The Equation 2x 2 Y 2 4x 4y 0 Transformed As 2x 2 Y 2 8x 8y 18 0 The Point To Which Origin Was Shifted Is

2

Moodle Swarthmore Edu

Math Drexel Edu

Solved 1 Expand F X Y X2 Xy Y2 In Powers Of X 1 Chegg Com

Solved Question 1 Range Of Glx Y V16 X2 Y2 Is Zlo Zs2 Chegg Com

Differential Equations

Jacobian If U X 2y 2 Z2 V X 2yz W 2x 2 Xy Find ꝺ U V W ꝺ X Y Z At The Point 1 1 0 Youtube

Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When

Antonleykin Math Gatech Edu

There Is An Electric Field E In The X Direction If The Work Done By The Electric Field In Moving A Charge Of 0 2 C Through A Distance Of 2 M

What Is The Equation Of The Tangent To The Curve Y 3x 2 X 1 At Point 1 3 Quora

Let L1 Be A Straight Line Passing Through The Origin And L2 Be The Straight Line X Y 1 If The Intercepts Made By The Circle X 2 Y 2

The Line 2x Y 1 0 Is Tangent To The Circle At The Point 2 5 And The Centre Of The Circles Lies On X 2y 4 The Radius Of The Circle Is

8 The Height And Radius Of A Right Circular Cylinder Chegg Com

Solved Ysin X Cos X Y 0 X Y Arctan Y 0 1 Find Dx Chegg Com

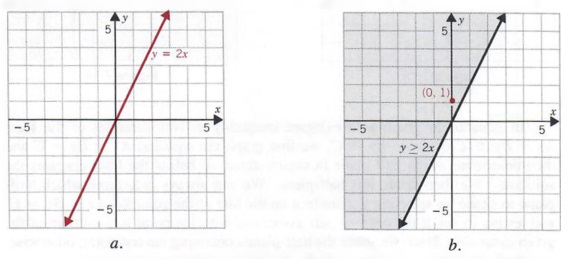
Graph Graph Equations With Step By Step Math Problem Solver

Tangent Lines And Implicit Differentiation

Solved If X 2xy Y 2 2 Them At The Point 1 1 Dy Dx Chegg Com

If V X 2y Y 2z Then Find E X Y Z

Calculus Show Function F X Y X 2 Y 2 2xy Is 1 1 By Inverse Function Theorem Mathematics Stack Exchange

If The Point 1 2 Lies On The Graph Of The Equation 2y Ax 4 Find The Value Of A And Hence Draw The Graph Of The Linear Equation

Analytic Geometry A Parabola Touches The Bisectors Of The Angles Formed By Lines X 2y 3 0 And 2x Y 3 0 At 1 1 And 0 2 Find Its Focus And Directrix Mathematics Stack Exchange

Solved A Rectangular Parallelepiped Has All Eight Vertices On The Ellipsoid X 2 3 Y 2 3 Z 2 1 Using The Symmetry Of The Parallelepiped About Each Of The Planes X 0 Y 0 Z 0 Write Down The Surface Area

If X 2 2xy 2y 2 1 Then Dydx At The Point Where Y 1 Is Equal To

Lf The Origin Is Shifted To The Point 1 2 Without Changing The Direction Of Axes The Equation X 2 Y 2 2x 4y 0 Becomes

Worked Example Evaluating Derivative With Implicit Differentiation Video Khan Academy

Solved Question 2 If Y Mx B Is The Equation Of The Tangent Line To The Curve X Quot 2xy Y X 39 At X 5 With A Negative Y Intercept Then E Course Hero

The Straight Line Y 2x 2 Intersects The Curve X Y 5 At Points A And B Given That A Lies Below The X Axis And The Point P Lies On Ab As Such That Ap Pb 3 1 What

Implicit Differentiation Calculator

What Is The Distance From The Point 1 2 3 To The Plane 2x 2y Z 1 Quora

57 Graphing Lines From Linear Equations

Answers Tutorial Sheet 5

2 3 Tangent Plane To A Surface Mathematics Libretexts

Implicit Differntiation Quiz Quizizz

Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When

Graph Graph Equations With Step By Step Math Problem Solver

Implicit Differentiation

If L1 Is The Line Of Intersection Of The Planes 2x 2y 3z 2 0 X Y Z 1 0 And L2 Is The

If X Y 2 And 2 X Y 1 5 Then

How To Prove X 2 Y 2 Xy If X Y X Y Quora

Msword Format